Spain

영상 : A Short Introduction to Entropy, Cross-Entropy and KL-Divergence

위 링크 영상에서 Entropy, Cross-entropy, KL-divergence 에 대해 이해하기 쉽게 설명을 해주고 있어, 정리 차원에서 작성해봅니다.

불확실성(Uncertainty) 과 bit

Entropy, Cross-entropy 의 개념은 미국의 수학자이자 암호학자인 Claude Shannon 의 1948년 논문 “A Mathematical Theory of Communication” 으로부터 시작되었습니다. 그는 논문에서 현재의 정보 이론(Information Theory)으로 불리는 개념을 처음 소개하였습니다. 디지털 통신에서 메세지는 bit 들로 이루어져 있는데, 알다시피 0 또는 1로 구성됩니다. 하지만 모든 bit 가 유용한 정보를 포함하지는 않습니다.

Shannon 은 자신의 이론에서 이렇게 설명합니다.

1 bit 의 정보를 전송하는 것은, 수신자의 불확실성을 2로 나누는 것을 의미한다.

직관적으로 잘 이해가되지는 않지만, 일기예보의 예를 들어보겠습니다. 내일 비가 올 확률이 50%, 맑을 확률이 50% 라고 합시다. 만약 기상청에서 내일 비가 온다고 예보를 했다면, 이는 우리의 불확실성을 2로 나눈 셈입니다. 같은 확률의 2가지 가능성이 있었는데, 예보로 인해 이것이 1로 줄었기 때문이죠. 따라서 기상청은 실제로는 1 bit 의 유용한 정보를 보낸 것이라고 할 수 있습니다. 이것은 실제로 이 정보가 어떻게 인코딩되었는지와는 무관합니다. “Rainy” 라는 문자열로 전달되었다면 데이터의 크기는 40 bit 이겠지만 실제 유용한 정보는 1 bit 인 것이죠.

그럼 내일의 날씨를 8 가지로 구분할 수 있다면 어떨까요?
예를 들면 ‘맑음, 약간 흐림, 흐림, 많이 흐림, 약간 비, 비, 많은 비, 천둥번개’ 라고 할 수도 있겠죠. 따라서 기상청이 내일의 일기 예보를 우리에게 보낸다면, 이는 우리의 불확실성을 8로 나눈 것이라고 할 수 있습니다. 8은 2의 3승이니까, 이 일기 예보는 3 bit 의 유용한 정보를 보낸 셈이죠.

이렇게 보면 ‘실제로 전달된 정보’의 bit 수를 계산하는건 간단해 보입니다. 불확실성을 줄여주는 인수(factor) 값에 로그2 를 씌워주면 되겠죠.
위 예제라면, 아래 식으로 설명될겁니다.

지금까지 설명한 것은 각각의 날씨들이 모두 같은 확률로 발생할 수 있다고 가정했는데요,
각각의 확률이 다르다면 어떻게 될까요? 예를 들어, 내일 비가 올 확률이 25%, 맑을 확률은 75% 라고 해봅시다.
이 때 기상청에서 내일 비가 올 것이라고 예보했다면, 이로 인해 우리의 불확실성은 1/2 이 아니라 1/4 로 줄었다고 할 수 있습니다.
불확실성이라는 개념이 조금 헷갈리지만, 50%, 50% 의 가능성을 가진 결과에서 하나를 예측한 것보다는 25%, 75% 의 가능성의 가진 결과 중에 25% 일 것이라고 예측하는 쪽이 더 많은 불확실성을 낮춰줬다고 말하는게 당연하겠죠.
만약에 비가 거의 오지 않는 사막에서 (비 올 확률 1%), 내일의 일기 예보가 ‘비’ 라고 한다면, 이는 불확실성이 1/100 로 훨씬 많이 줄어들었다고 할 수 있을 것입니다. 즉, 같은 ‘비’ 예보라고 하더라도, 비 올 확률이 50% 인 장소에서의 의미와, 1% 인 장소에서의 의미는 다를 것입니다. 당연히 1% 인 곳에서는 더 많은 불확실성이 해소된거죠.

Entropy

위 설명을 공식화해서 설명해보면,

불확실성이 감소되는 크기는 어떤 이벤트의 발생 확률의 역수와 같다.

라고 할 수 있습니다. 위 예제의 경우, 25% 의 역수이므로,

$ 1 / 0.25 = 4$ 이고, 따라서 $ log_2(4) = 2 $ 이니까 2 bit 의 정보가 필요한게 됩니다. 이 때 역수의 log 는 - 를 붙이는 것과 같으니까,

$ log_2(4) = -log_2(0.25)$

로 정리할 수 있겠네요.

만약 위 예제에서 기상청이 내일 날씨가 맑을거라고 예보하는 경우, 불확실성은 그렇게 많이 낮아지지 않을겁니다.

$ -log_2(0.75) = 0.41 $

즉, 0.41 bit 가 됩니다. 0.41 bit 만큼의 정보를 얻을 수 있다는 뜻이죠.

그럼 기상청으로부터 얻을 수 있는 정보의 평균값은 얼마일까요? 각각의 이벤트에 대한 기대값을 계산해보면,

$ 75\% * 0.41 + 25\% * 2 = 0.81 \text{ bits} $

즉, 평균적으로 우리는 매일 기상청으로부터 0.81 bit 의 정보를 얻을 수 있다고 할 수 있습니다.
이것이 바로 Entropy 입니다. Entropy 는 어떤 이벤트가 얼마나 불확실한지 를 설명하는 아주 훌륭한 방법입니다.

위 공식이 완전히 이해가 되죠? 요약하자면,

Entropy 는 주어진 확률 분포 p 에서 하나의 샘플로부터 얻을 수 있는 정보의 평균량이다.

라고 할 수 있을 것입니다. 이는 해당 확률 분포가 얼마나 예측하기 힘든지를 의미합니다.
만약 우리가 거의 항상 날씨가 맑은 사막 한가운데에 살고 있다면, 일기 예보로부터 얻을 수 있는 정보는 많지 않습니다.
Entropy 는 거의 0에 가깝겠죠?
반대로 날씨가 변화무쌍한 곳이라면 Entropy 값은 훨씬 클 것입니다.

Cross-entropy and KL Divergence

그럼 Cross-entropy 는 뭔지 얘기해볼께요. 사실 아주 간단한 개념입니다.
바로 메세지 길이의 평균값 입니다. 위에서 설명했던 8가지 날씨 예제에서, 기상청이 아래와 같은 3 bit 의 정보를 사용한다고 해보죠.

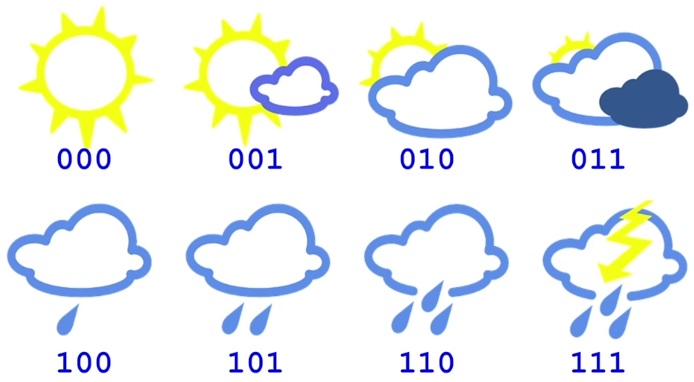
이 경우 메세지의 평균 길이는 당연히 3 bit 입니다. 그게 Cross-entropy 입니다.
하지만 이것은 각각의 확률이 같다고 가정한 경우이고, 만약 아래 그림처럼 각각 날씨에 대한 확률이 다른 경우는 어떨까요?

이 경우 Entropy 를 계산해보면,

즉, 실제 유용한 정보는 2.23 bit 뿐임을 알 수 있습니다. 그럼 아래처럼 변경하면 어떨까요?

이제 각각의 날씨에 대한 메세지의 길이를 달리 했습니다.
이렇게 하면 연속된 bit 들에 대해서도 간단하게 해석이 가능해집니다.
예를 들어 011100 이라는 메세지는 01 + 1100 만으로 분리 가능하기 때문이죠.
이때 Cross-entropy 를 다시 계산해보면,

$ 35\% * 2 + 35\% * 2 + 10\% * 3 + \text{…} + 1\% * 5 = 2.42 \text{ bits} $

이렇게 Cross-entropy 를 개선시켰습니다. 하지만 3 bit 보다는 낫지만 2.23 bit 까지는 낮추진 못했죠.
아무튼 이번엔 이 방식을 다른 장소에 적용해보면 어떨까요? 아래처럼 항상 비가 오는 곳이라고 해보죠.

이 때의 Cross-entropy 를 계산해보면, 4.58 bit 라는 값이 나오게 됩니다.

굉장히 안좋은 결과네요. 거의 entropy 의 2 배에 가깝습니다.
다시 말하면, 이 경우 평균적으로 4.58 bit 가 전송되지만 실제로는 2.23 bit 만이 유용하다는 의미입니다.
이는 우리의 코드가 날씨의 분포에 대해서 가정(assumption) 을 내포하고 있기 때문입니다.
예를 들어, 맑은 날씨를 2 bit 메세지로 전송하겠다는 것은 최소한 4일에 한 번(2 의 2 승)은 날씨가 맑을 것이라는 걸 내포하고 있습니다.
즉, 우리의 코드는 25% 확률로 날씨가 맑을 것이라는 암묵적인 예측을 하고 있는 셈입니다. 그게 틀린다면 우리의 코드는 최적화될 수 없겠죠.

따라서 예측된 분포 q 는 실제 분포 p 와 차이가 발생할 수 밖에 없습니다.

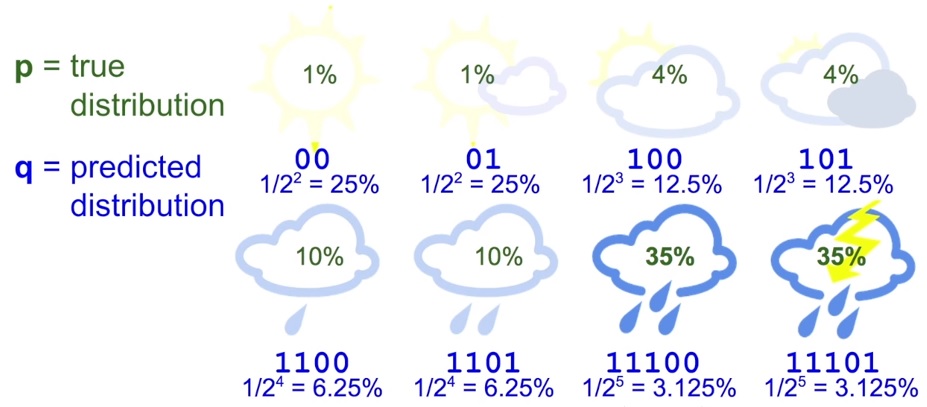
이제 Cross-entropy 를 실제 확률 분포 p 와, 예측된 확률 분포 q 의 공식으로 설명이 가능해집니다.

보시다시피 Entropy 공식과 비슷하지만, 실제 분포 p 의 log 대신 예측된 분포 q 의 log 를 사용하고 있습니다.
여기서 $ log_2(q) $ 는 메세지의 길이죠.
만약 우리의 예측이 완벽하다면, 즉 예측된 분포가 실제 분포와 동일하다면, Cross-entropy 는 Entropy 와 같은 값을 가질 것입니다.
하지만 분포가 차이날수록 Cross-entropy 는 Entropy 보다 더 큰 값이 되겠죠.

이와 같이 Cross-entropy 와 Entropy 의 차이를 Relative Entropy 라고 부르고, 더 일반적으로
Kullback-Leibler Divergence (KL Divergence) 라고 부릅니다.

공식으로 적어보면,

위의 예제에서, Cross-entropy 는 4.58 bit 이고 Entropy 가 2.23 bit 였으니까 KL Divergence 는 2.35 bit 가 되겠네요.

Cross-entropy in Machine Learning

이미지 분류 모델에서, 모델이 예측한 결과를 q 라고 생각하면 됩니다.
그리고 실제 분포 p 는 주어진 label 로부터 계산하면 되겠죠?

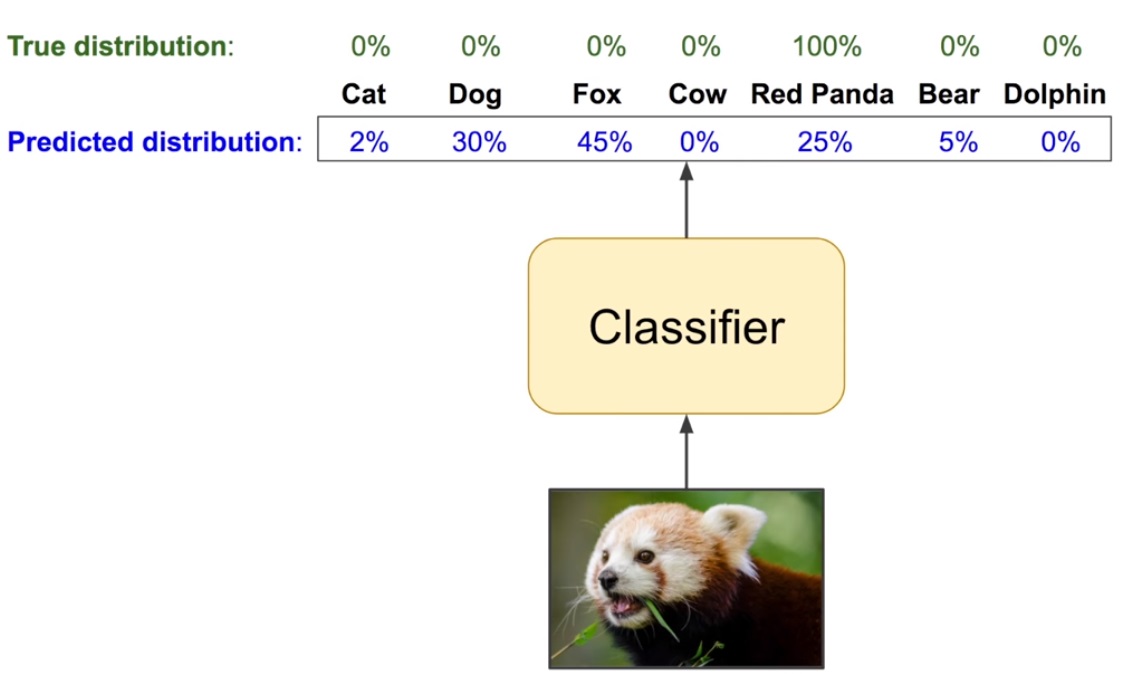
분류 모델에서 왜 Cross-entropy Loss 가 사용되는지 이제 잘 알 수 있을 것입니다.

여기서 이진 log 가 아닌 자연 log 가 사용되었는데, 이는 모델 학습 시 차이가 없기 때문입니다.
이진 log 는 자연 log 를 상수로 나눈 것일 뿐이니까요.

위 그림의 경우 Cross-entropy loss 값은 $ -log(0.25) = 1.386 $ 으로 굉장히 큰 값을 나타내고 있네요.
예측된 분포가 실제 분포와 같아질수록 loss 는 0 에 가까워 질 것입니다.

끝.

원본 : How to build Ensemble Models in machine learning?

지난 12개월 간 다양한 머신 러닝 해커톤에 참여해왔다. 시합이 끝나면 항상 1등의 솔루션을 확인해보는데, 보다보면 굉장한 insight 를 받기도 해서 차후 시합에 큰 도움이 되곤 했다.
우승자들의 대부분은 잘 튜닝된 개별 모델의 앙상블(Ensemble) 과 더불어 feature engineering 을 사용하고 있었다. 이 두 방법을 잘 기억하기를 조언한다. 머신 러닝에 있어서 이 것들을 잘 사용하는 것이 아주 중요하기 때문이다.
나는 대부분의 경우 feature engineering 은 잘 사용해왔지만, 앙상블은 사용하지 않았다. 만약 당신이 초보자라면 앙상블 모델에 최대한 빨리 익숙해지는 것이 좋을 것이다. (어쩌면 무의식 중에 이미 적용중이었을 수도 있다!)

이 포스트에서 앙상블 모델링의 기초에 대해 설명하고자 한다. 그리고 나서 앙상블의 장단점을 살펴보고, 실습을 제공할 것이다.

1. Ensemble 이란?

일반적으로 앙상블이란 2개 이상의 알고리즘 - base learner 라고 함 - 들을 결합해서 사용하는 기술을 의미한다. 모든 base learner 들의 예측 결과를 조합하여 사용하기 때문에 전체 시스템을 보다 탄탄하게 해준다. 여러명의 주식 거래자들이 한 방에 모여 주가가 오를지 내릴지를 토론하여 결정하는 것과 마찬가지라고 생각하면 되겠다.

각각의 거래자들이 모두 다른 정보와 이해를 가지고있기 때문에, 문제 상황으로부터 결론에 이르기까지의 공식은 다 다를 것이다. 따라서 주식 시장에 대한 각자의 이해를 바탕으로 다양한 주가 예측이 나오게 된다.

이제 최종 결론을 내릴 때가 되면 모든 다양한 예측들을 함께 고려해봐야할 것이다. 이로 인해 우리의 최종 결론은 더욱 탄탄(robust)하고, 정확하고, 덜 편중(biased)된 방향으로 결정될 수 있다. 최종 결론은 거래자 개인의 판단에 기반한 결론과 정 반대의 내용이 될 지도 모른다.

또 다른 예로 구직자의 인터뷰를 들 수 있다. 구직자가 가진 능력에 대한 최종 판단은 인터뷰 진행자들의 모든 피드백에 기반하여 결정된다. 인터뷰 진행자 한 명만으로는 요구 기술과 특성 각각에 대한 테스트를 모두 수행하지는 못할 수 있다. 하지만 여러명의 인터뷰 진행자들의 복합적인 피드백으로 인해 구직자에 대한 더 올바른 평가가 이루어 질 수 있는 것이다.

2. Types of ensembling

더 세부적으로 진행하기 전에 꼭 알아야하는 기본 컨셉들이 있다:

• Averaging :
  모델들의 예측 결과에 대한 평균을 취하는 것으로, regression 문제나 classification 확률 예측 문제에 모두 사용된다.

• Majority vote :
  classification 문제를 해결할 때, 각각의 모델이 선정한 결과 중 최대 빈도로 선택된 결과를 취하는 방식이다.

• Weighted average :
  Average 값들에 모델 별 가중치를 두는 방식이다.

여러 개의 모델들을 조합하는 방법은 셀 수 없이 많을 것이다. 하지만 주로 사용되는 기술들을 소개한다:

1. Bagging
   Bagging 은 Bootstrap aggregation 이라고도 불린다. Bagging 을 이해하기 위해서는 먼저 bootstraping 을 이해할 필요가 있다. Bootstraping 은 n 개의 행을 가진 원본 dataset 으로부터 n 개의 행을 선택하는 샘플링 기법이다. 핵심은 각각의 행이 선택될 때 동일한 확률로 선택된다는 것이다.
   Original dataset
   1st sampling
   2nd sampling
   3rd sampling
   랜덤하게 선택하기 때문에, 위와 같이 중복 선택이 허용된다.

   동일한 원본 data 로부터 여러개의 bootstrapped sample 들을 추출할 수 있는데, 추출된 sample 로부터 또 다시 bootstraping 을 하면 tree 구조의 많은 sample set 을 구성할 수 있다. 그러한 sample set 을 기반으로 majority vote 나 averaging 기법을 사용해서 최종 예측을 얻을 수 있다. Bagging 이란 이렇게 동작하는 것이다.

   여기서 눈여겨 보아야 할 것은, bagging 을 통해 분산(variance)를 줄일 수 있다는 점이다. Random forest 가 사실 이러한 컨셉을 사용하는데, Random forest 는 한 발 더 나아가 각각의 bootstrap 된 sample 들의 feature subset 까지 랜덤하게 추출함을 통해 분산을 줄인다. 이를 통해 학습 데이터를 구분(split) 할 수 있다.

2. Boosting
   Boosting 은 여러개의 알고리즘을 순차적으로 적용하는 기법으로, 첫 번째 알고리즘이 전체 dataset 에 대한 학습을 진행하고, 다음 알고리즘들은 첫 번째 알고리즘이 실패한(남긴, residuals) 데이터에 맞추어 생성되는 방식이다. 따라서 다음 알고리즘들은 이전 모델이 잘 예측하지 못한 데이터에게 더 큰 가중치를 두게 된다.
   이는 전체 dataset 에 대한 성능은 좋지 않지만, 특정 부분에 대한 성능은 좋은 learner 들의 집합으로 이루어진다. 따라서 각각의 모델이 모여 앙상블 전체의 성능을 향상(boost) 시키는 것이다.
   여기서 중요한 부분은, boosting 은 편중(bias) 를 줄이는 데에 집중한다 는 점이다. 이로 인해 boosting 은 오버피팅을 유발하기 쉽다. 따라서 boosting 사용 시, 오버피팅을 피하기 위한 파라메터 튜닝이 굉장히 중요하다.
   Boosting 의 대표적인 예제로는 XGBoost, GBM, ADABOOST 등이 있다.

3. Stacking
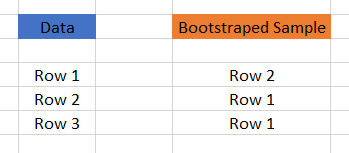
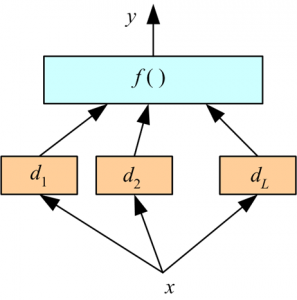   Stacking 은 여러개의 머신 러닝 모델들을 쌓아서 각각의 모델이 예측 결과를 상위 레이어의 모델에 전달하고, 최상위의 모델이 최종 결론을 도출하는 방식이다. 위 그림에는 두 개의 머신 러닝 모델들이 존재하고 있다:

   • 하위 레이어의 모델들(d1, d2, d3) 는 원본 입력 feature들(x) 를 취한다.
   • 최상위 모델 f() 는 하위 레이어 모델의 출력을 받아 최종 출력을 예측한다.
   • 주목할 점은 예측된 결과 값들이 학습 data 로 사용된다는 점이다.

위에서는 2 개의 레이어만 사용되었지만, 다양한 수의 레이어가 사용될 수 있고, 레이어 내의 모델 역시 개수에 제한이 없다. 모델들을 선택함에 있어 두 가지 핵심 요건이 있는데:

• 개별 모델들은 정해둔 정확도 요건(criteria)을 충족시킬 것.
• 개별 모델의 예측 값은 다른 모델의 예측과 큰 연관도(correlation)가 없어야 한다.

최상위 모델은 하위 모델의 예측 결과를 입력값으로 받고 있는데, 이 최상위 모델 또한 아래와 같은 단순한 모델로 대체될 수 있다:

• Averaging
• Majority vote
• Weighted average

3. Ensemble 의 장단점

3.1 장점

• 앙상블은 모델의 정확도를 높이고, 대부분의 case 에 대해 잘 동작한다고 입증된 방식이다.
• 거의 모든 머신 러닝 해커톤에 있어서, 1위를 하는데 필수적이다.
• 앙상블은 모델을 더욱 탄탄하고 안정적이게 해주고, 따라서 대부분의 시나리오에서 괜찮은 성능을 보장해준다.
• Data 에 내재하는 선형적이고 단순한 관계 뿐 아니라 비선형적인 복잡한 관계까지 뽑아내는 데에 앙상블을 사용할 수 있다.
  2 개의 다른 모델을 사용해서 하나의 앙상블을 구성하면 된다.(?)

3.2 단점

• 앙상블은 모델의 해석력(interpretability)을 떨어뜨리고, 결국 비지니스 insight 를 이끌어내기가 굉장히 힘들어 질 수 있다.
• 시간이 많이 걸리고, 실시간 어플리케이션 용으로는 적합하지 않을 수 있다.
• 앙상블을 구성하는 모델을 잘 선택하는 방법을 익히는 것이 어렵다.

4. 예제

생략

5. 더 알아보기

• 5 Easy questions on Ensemble Modeling everyone should know
• 40 Questions to ask a Data Scientist on Ensemble Modeling Techniques (Skilltest Solution)

CRF 란?

저스틴 비버의 하루 일상을 순서대로 찍은 사진들이 있다고 상상해보자.
우리는 각각의 사진에 한 단어로 설명(라벨)을 달고자 한다. (예> 식사 사진, 수면 사진, 운전 중 등등)
어떻게 하면 될까?

한가지 방법은 사진들이 가지는 순서에 대한 정보는 무시하고 각 사진 자체만으로 분류를 해보는 것이 될 수 있겠다. 예를 들어 라벨이 달린 한 달 치의 사진이 주어졌다고 하면, 아침 6시 쯤에 찍힌 어두운 사진들은 ‘수면’ 과 연관이 있는 사진들이고, 밝은 색깔이 많이 포함된 사진은 ‘춤’ 에 대한 사진, 자동차가 나온 사진들은 ‘운전’ 사진이라는 등의 사실을 배울 수 있을 것이다.

하지만 순서에 대한 관점을 무시하면 많은 양의 정보를 잃게 된다. 예를 들어 입만 크게 나온 사진이 있다고 하자. 그건 노래하는 사진일까 밥 먹는 사진일까? 만약 이전의 사진이 저스틴 비버가 밥을 먹거나 요리하는 사진이었다면, 그 입 사진은 ‘먹는’ 행위에 관한 사진일 가능성이 더 높을 것이다. 하지만 이전 사진이 저스틴 비버가 노래나 춤 추는 사진이었다면, 입 사진도 마찬가지로 ‘노래하는’ 사진일 가능성이 높다.

Part-of-Speech Tagging

part-of-speech tagging 를 예로 좀 더 자세히 살펴보도록 하자.
POS tagging 의 목적은 한 문장의 어휘들의 품사를 달아주는 것이다. (ex> 명사, 동사, 형용사, 명사)
예를 들어 ‘Bob drank coffee at Starbucks.’ 라는 문장은 ‘Bob(명사) drank(동사) coffee(명사) at(전치사) Starbucks(명사)’ 가 될 것이다. 그럼 이제 CRF 를 이용해서 POS tagging 을 해보자. 먼저 다른 classifier 들과 마찬가지로 feature function $f_i$ 들을 정의해야 한다.

Feature functions in a CRF

CRF 에서 각각의 feature function 은 아래와 같은 입력들을 받는 함수이다:

• s : 문장
• i : 단어의 문장 내 인덱스
• $l_i$ : 현재 단어의 라벨
• $l_{i-1}$ : 이전 단어의 라벨

그리고 출력 값은 실수 값이 된다.(하지만 실제로는 0 또는 1 인 경우가 많다.)

참고 : 본 포스팅에서는 문장 전체에 대한 라벨이 아니라 현재 단어와 이전 단어의 라벨만 사용하도록 제한하고 있다. 이것은 linear-chain CRF 의 일종이라고 할 수 있다. 설명의 편의를 위해 범용적인 CRF 에 대한 내용은 생략하고자 한다.

Feature 를 Probabilties 로.

이제 각각의 feature function $f_j$ 에 weight $\lambda_j$ 를 할당해 보자.(데이터로부터 이 weight 들을 어떻게 학습하는 지는 아래에 설명하겠다.)
문장 s 가 주어졌을 때, 문장 내 모든 단어에 대한 weighted feature 값을 더하여 s 에 라벨 l 이 부여될 수 있는지 점수를 매길 수 있다.

(첫 번째 시그마는 각각의 feature function $f$ 에 대한 것이고, 안쪽 시그마는 $i$ 위치의 단어 각각에 대한 연산이다.)

그 다음 지수 연산(exponentiating)과 정규화(normalizing)를 통해 이 점수를 확률 $p(l | s)$ 로 환산할 수 있다.

Feature Function 예시

그럼 이 feature function 들은 어떻게 생겼을까? POS tagging 의 feature 들은 다음과 같을 수 있다:

• $$f_1(s, i, l_i, l_{i-1}) = \begin{cases} 1 & \mbox{if }l_i = \text{부사(ADVERB)} \mbox{ and the ith word ends in “-ly”} \\ 0 & \mbox{otherwise.} \end{cases}$$
  • 이 feature 에 대한 weight $\lambda_1$ 값이 양수이고 큰 경우, 이 feature 는 -ly 로 끝나는 단어를 ‘부사’ 로 라벨링할 거라는 의미가 될 것이다.
• $$f_2(s, i, l_i, l_{i-1}) = \begin{cases} 1 & \mbox{if } i = 1, l_i = 동사(VERB), \mbox{ and the sentence ends in a question mark} \\ 0 & \mbox{otherwise.} \end{cases}$$
  • 마찬가지로 feature 에 대한 weight $\lambda_2$ 값이 양수이고 큰 경우, ? 로 끝나는 문장의 첫 단어를 ‘동사’ 로 라벨링하고자 할 것이다.
• $$f_3(s, i, l_i, l_{i-1}) = \begin{cases} 1 & \mbox{if }l_{i-1} = \mbox{형용사(ADJECTIVE)} \mbox{, and }l_i = \mbox{명사(NOUN)} \\ 0 & \mbox{otherwise.} \end{cases}$$
  • weight 가 양수 인 경우, 이 feature 는 형용사 뒤에는 명사가 온다는 것을 의미한다.
• $$f_4(s, i, l_i, l_{i-1}) = 1 \mbox{ if }l_{i-1} =\mbox{ 전치사(PREPOSITION) and }l_i = \mbox{전치사(PREPOSITION).}$$
  • 이 함수에 대한 음수의 weight $\lambda_4$ 는 전치사 뒤에는 전치시가 오면 안되다는 것을 의미한다. 따라서 그런 라벨링이 발생하지 않도록 할 수 있을 것이다.

이게 끝이다!
정리해보면 CRF 를 만들기 위해서는,

1. feature function 몇 개를 정의해주고, (feature function 은 전체 문장, 현재 위치, 그리고 주변의 라벨 값을 참조한다.)
2. weight 를 할당하고
3. 전체를 몽땅 더한 다음,
4. 필요하면 그 값을 확률로 환산하면 된다.

이제 CRF 이 다른 머신 러닝 기술들와 어떻게 다른지 비교해보도록 하자.

Smells like Logistic Regression…

CRF 의 아래 식은 왠지 친숙해 보일 수도 있다. 궁금하면 여기

왜냐하면 CRF 는 근본적으로 Logistic Regression 의 순차 버전(sequential version)이기 때문이다.

Logistic Regression 이 분류(claasification) 을 위한 log-linear 모델인데 반해,
CRF 는 순차적인 라벨링(sequential labels) 을 위한 log-linear 모델이다.

Looks like HMMs…

HMM(Hidden Markov Model) 도 POS tagging(또한 일반적인 순차 라벨링) 에 사용될 수 있는 모델임을 기억하자.
CRF 가 라벨링 점수를 계산하기 위해 여러 개의 feature function 을 다 같이 사용하는데 비해,
HMM 은 라벨링을 위해 생성적(generative) 방식을 취한다. 그 식은 아래와 같다:

이 때,

• $ p(l_i | l_{i-1})$ 는 전이 확률(transition probabilities) - 예> 전치사 뒤에 명사가 나올 확률
• $ p(w_i | l_i)$ 는 출력 확률(emission probabilities) - 예> ‘명사’ 라벨이 ‘아빠’ 를 도출할 확률

그럼 HMM 과 CRF 는 어떻게 다른가?
CRF 가 더 강력하다!
CRF 는 HMM 이 할 수 있는 모든 것을 모델링할 수 있고, 그것보다 더 많은 일을 해낸다. 왜 그런지는 아래를 살펴보자.

HMM 확률 식에 log 를 취하면 아래와 같다.

이 log-확률을 2진(binary) 전이, 출력 feature 들에 할당된 weight 라고 간주하면, 위 식은 CRF 의 log-linear 형태와 완전히 일치한다. 다시 말해, 어떠한 HMM 이라도 그와 동일한 CRF 를 구현할 수 있다는 뜻이다. 그 방법은 아래와 같다.

• HMM 의 전이 확률 $p(l_i = y | l_{i-1} = x)$ 각각에 대해 CRF 전이 feature 를 아래처럼 정의한다.
  $f_{x,y}(s, i, l_i, l_{i-1}) = 1 \text{ if }l_i = y \text{, and }l_{i-1} = x$
  그리고 각 feature 에 다음과 같은 weight 를 부여한다.
  $w_{x,y} = \log p(l_i = y | l_{i-1} = x)$
• 위와 유사하게, HMM 의 출력 확률 $p(w_i = z | l_{i} = x)$ 각각에 대해 CRF 출력 feature 를 아래처럼 정의한다.
  $g_{x,y}(s, i, l_i, l_{i-1}) = 1 \text{ if }w_i = z\text{, and }l_i = x$
  그리고 각 feature 에 다음과 같은 weight 를 부여한다.
  $w_{x,z} = \log p(w_i = z | l_i = x)$

그러면 이 feature function 들을 사용하여 계산된 $p(l|s)$ 점수는 해당하는 HMM 에 의해 계산된 점수에 정확히 비례하게 되고, 따라서 모든 HMM 은 특정 CRF 로 표현이 가능해진다.

하지만 CRF 훨씬 풍부한 라벨 분포 set 를 모델링할 수 있는데, 이 이유는 다음과 같다.

• CRF 는 훨씬 많은 수의 feature set 를 정의할 수 있다. HMM 은 태생적으로 지엽적(local) 속성을 가진다. 왜냐면 HMM 은 2진 전이, 출력 feature function 만 사용 가능하고, 이로 인해 각 단어는 오직 현재의 라벨에, 그리고 각 라벨은 바로 이전의 라벨에만 의존하게 되기 때문이다. 이에 반해 CRF 는 좀더 전역적(global) feature 들을 사용할 수 있다. 예를 들어 위에서 보여준 POS tagger 의 feature 들 중 하나는 문장의 끝이 ? 인 경우 문장의 제일 첫 단어가 동사 로 태깅될 확률을 높이고 있다.
• CRF 는 임의(arbitrary)의 weight 값들을 가질 수 있다. HMM 의 확률 값들은 어떤 조건 - 예를 들면, $ 0 <= p(w_i | l_i) <= 1, \sum_w p(w_i = w | l_1) = 1$ - 을 반드시 충족시켜야만 한다. 그에 비해 CRF 의 weight 는 아무 제약이 없다.
  $\log p(w_i | l_i)$ 는 어떠한 값이든 될 수 있다.

Weight 의 학습

CRF 에서 weight 를 어떻게 학습시키는지에 대한 질문으로 다시 되돌아가자. gradient ascent (짜잔) 를 사용하는 것이 하나의 방법이 될 수 있다.

학습 데이터(문장들과 그에 대한 POS 라벨들)가 충분히 있다고 가정해보자. 먼저 CRF 모델의 weight 들을 임의의 값으로 초기화 한다. 이 무작위 weight 값들을 정답으로 바꿔나가려면 각각의 학습 데이터에 다음과 같은 작업을 해주면 된다.

• 각각의 feature function $f_i$ 에서 학습 데이터의 log 확률에 대한 gradient 를 계산한다. $\lambda_i \text{ : }\frac{\partial}{\partial w_j} \log p(l | s) = \sum_{j = 1}^m f_i(s, j, l_j, l_{j-1}) - \sum_{l’} p(l’ | s) \sum_{j = 1}^m f_i(s, j, l’_j, l’_{j-1})$
• gradient 의 첫 번째 term 은 true 라벨을 갖는 feature $f_i$ 의 분포를, 두 번째 term 은 현재 모델에서 feature $f_i$ 의 expected 값의 분포를 나타냄을 주목하자.
• $\lambda_i$ 를 gradient 방향으로 이동시킨다 :
  $\lambda_i = \lambda_i + \alpha [\sum_{j = 1}^m f_i(s, j, l_j, l_{j-1}) - \sum_{l’} p(l’ | s) \sum_{j = 1}^m f_i(s, j, l’_j, l’_{j-1})]$ where $\alpha$ is some learning rate.
• 특정 조건(더 이상 갱신이 안된다던가)에 도달할 때까지 위의 작업을 반복한다.

최적 라벨 찾기

우리의 CRF 모델을 학습시켰고 이제 새로운 문장이 입력된다고 생각해보자. 라벨링은 어떻게 되나?

단순한 방법은 모든 가능한 라벨 l 에 대한 $p(l | s)$ 를 계산하고, 이 확률을 최대화 시키는 라벨을 고르는 것이 될테다. 하지만 m 길이의 문장과 k 개의 tag 셋이 있다면 총 $k^m$ 개의 조합이 가능하기 때문에, 이 방식은 지수승의 연산을 필요로 한다.

더 좋은 방법이 있다. (linear-chain) CRF 는 optimal substructure 속성을 만족하기 때문에, (polynomial-time 복잡도의) 동적 프로그래밍 알고리즘으로 최적 라벨을 찾을 수 있다. 이는 HMM 에 Viterbi 알고리즘을 적용하는 것과 유사하다.

좀 더 재밌는 응용

사실 part-of-speech tagging 은 좀 지루하고, 다른 POS 태거도 이미 많다. 실 생활에서 CRF 는 어디다가 써먹을 수 있을까?

트위터에서 사람들이 크리스마스에 받은 선물의 타입을 마이닝하고 싶다. 고 해보자.

그러면 문장에서 어느 단어가 선물에 해당하는지 어떻게 찾아낼 수 있나??!!1

위와 같은 그래프를 만들기 위해 나는 그냥 “크리스마스에 XXX 가 갖고싶어요.” 와 “크리스마스에 XXX 를 받았어요!” 형태의 문장을 검색했을 뿐이다. 하지만 더 세련된 CRF 버전으로, part-of-speech 에서의 품사 같이 GIFT 라는 태그 (한 발 더 나가면 GIFT-GIVER, GIFT-RECEIVER 를 이용해 선물을 준사람과 받은사람의 정보까지) 를 사용해서 이것을 POS 태깅 문제처럼 해결해 볼 수 있을 것이다. 그 때 feature 는,

• “이전 단어가 GIFT-RECEIVER 이고 그 이전 단어가 ‘gave’ 라면, 현재 단어는 GIFT 임”
• “다음 두 단어가 ‘for Christmas’ 면 현재 단어는 GIFT 임”

와 같은 형태가 될 수 있을 것이다.

마무리

좀더 ‘랜덤한’ 생각을 나열하고 끝내고자 한다.

• 이 포스트에서는 CRF 를 사용한 그래픽 모델 프레임웍에 대한 내용은 일부러 스킵했다. 왜냐면 CRF 의 기본을 이해하는데는 큰 도움이 되지 않기 때문이다. 하지만 더 알고싶다면 Daphne Koller 가 공짜로 가르쳐주는 온라인 강좌를 들어보시길.
• 아니면 CRF 를 적용한 많은 NLP 응용 분야(POS 태깅이나 named entity extraction등)에 관심이 있다면 Manning 과 Jurafsky 가 강의를 하고 있다. (링크가 있었는데 깨짐. http://www.nlp-class.org)
• 또한 CRF/HMM 과 Logistic Regression/Naive Bayes 간의 유사점에 대해 조금 더 꾸며봤다. 아래 이미지를 참고바람.

출처 : introduction to conditional random fields

jsMath(TeX) in markdown

마크다운 문서에서는 아래와 같이 $$ 부호 내에 입력하면 자동 전환됨.

$$
y = x^2
$$

결과 :
$y = x^2$

1. 산술 함수

2. 미분

3. 근호

4. 순열과 조합

5. 집합

6. 위, 아래, 전치, 후치, 첨자

7. 기타

f(n)=
\begin{cases}
n/2, & \mbox{if }n\mbox{ is even} \\
3n+1, & \mbox{if }n\mbox{ is odd}
\end{cases}

$f(n)= \begin{cases} n/2, & \mbox{if }n\mbox{ is even} \\ 3n+1, & \mbox{if }n\mbox{ is odd} \end{cases}$