정의

In statistics, Gibbs sampling or a Gibbs sampler is a Markov chain Monte Carlo (MCMC) algorithm for obtaining a sequence of observations which are approximated from a specified multivariate probability distribution, when direct sampling is difficult. This sequence can be used to approximate the joint distribution (e.g., to generate a histogram of the distribution); to approximate the marginal distribution of one of the variables, or some subset of the variables (for example, the unknown parameters or latent variables); or to compute an integral (such as the expected value of one of the variables). Typically, some of the variables correspond to observations whose values are known, and hence do not need to be sampled.

Gibbs sampling is commonly used as a means of statistical inference, especially Bayesian inference. It is a randomized algorithm (i.e. an algorithm that makes use of random numbers), and is an alternative to deterministic algorithms for statistical inference such as the expectation-maximization algorithm (EM).

As with other MCMC algorithms, Gibbs sampling generates a Markov chain of samples, each of which is correlated with nearby samples. As a result, care must be taken if independent samples are desired. Generally, samples from the beginning of the chain (the burn-in period) may not accurately represent the desired distribution and are usually discarded. If necessary, one possible remedy is thinning the resulting chain of samples (i.e. only taking every nth value, e.g. every 10th value). It has been shown, however, that using a longer chain instead (e.g. a chain that is n times as long as the initially considered chain using a thinning factor of n) leads to better estimates of the true posterior. Thus, thinning should only be applied when time or computer memory are restricted.[1]

hello $y = \frac{x ^ 2}{2} K\left(1-\sqrt{x^3 - 8}\right)$ world

출처 : Gibbs Sampling

정의

난수를 이용하여 함수의 값을 확률적으로 계산하는 알고리즘.

핵심 아이디어

이론상 determistic 할지도 모르는 문제에 대해 randomness 를 사용하여 해결한다!

주로 물리/수학적 문제들에 대해 다른 방법으로 해결할 수 없는 경우에 사용한다.(ㅋㅋ)

주요 적용 분야

1. 최적화 문제
2. numerical integration (수치적 미분?)
3. 확률 분포로부터 draw 를 생성 (generating draw from probability distribution)

어떻게 동작하나?

일반적으로 아래 패턴으로 동작함.

1. 입력 가능한 데이터의 도메인을 정의한다.
2. 해당 도메인에 대한 확률 분포로부터 랜덤 데이터를 생성
3. 입력 데이터에 대한 deterministic 계산을 수행
4. 결과 수집

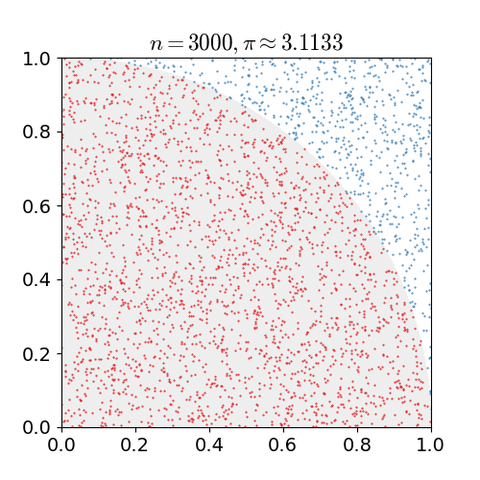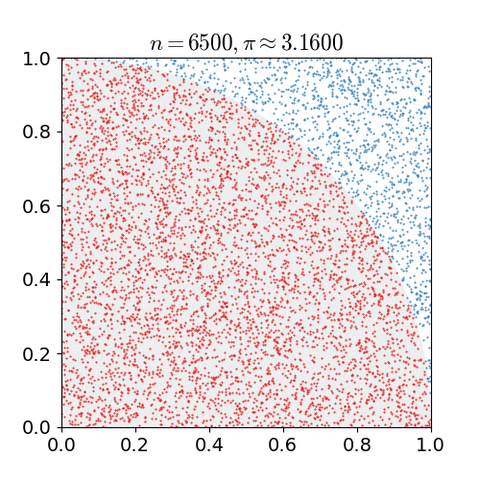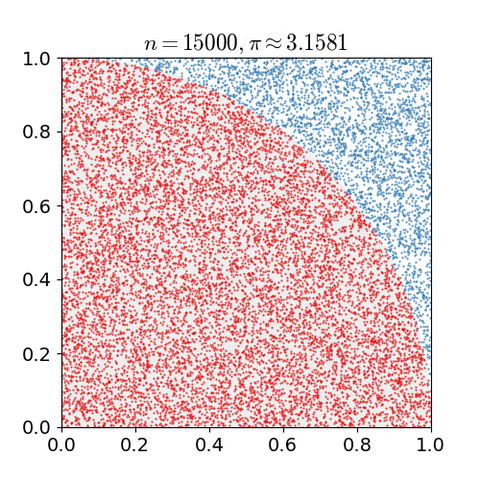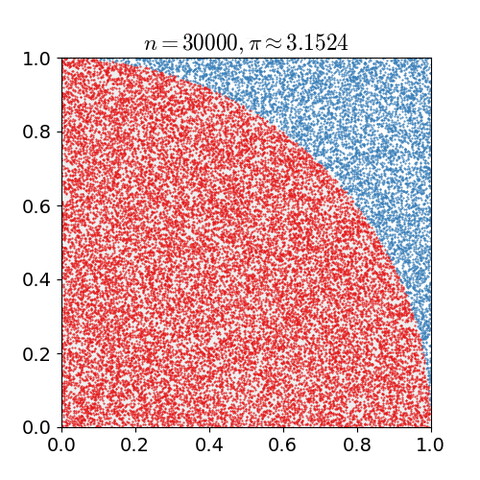
예를 들어, (x,y) 그래프의 1 사분면에 (0, 0) 을 중점으로 하고 반지름이 1 인 원이 있다고 생각해보자. 원의 넓이는 π/4 일 것이다.
이 때 Monte Carlo Method 를 이용해 π 값을 근사해 보면,

1. 한 변의 길이가 1인 정사각형을 그리고, 그 안에 반지름이 1 인 원을 그린다. (1/4 원)
2. 균등한 크기의 물체를 사각형 안에 균등하게 흩뿌린다.(uniformly scatter)
3. 원 안에 들어간 물체의 갯수와 전체 갯수를 센다.
4. 원 안에 들어간 물체의 갯수와 전체 갯수의 비율은 두 영역의 비율과 같으므로, 즉 π/4 가 된다.
   해당 비율에 4을 곱해서 π 의 근사치를 구할 수 있다.

여기서 중요한 포인트 2가지.

1. 흩뿌릴 때 균등하게 분포되지 않으면 결과가 좋지 않을 것이다.
2. 입력 데이터의 갯수가 많아야 한다. 많을 수록 결과가 개선될 것이다.

Monte Carlo Method 를 적용하기 위해서는 많은 수의 랜덤 값들이 요구되는데, 이로 인하여 pseudorandom number generator 의 개발에 박차를 가하게 되었다. pseudorandom number generator 는 기존에 통계적 샘플링에서 주로 사용되던 랜덤 숫자 테이블(table of random numbers) 대비 훨씬훨씬 성능이 좋았다.

출처 : Monte Carlo method

Useful queries

• $ne
  desc != ''

  { desc: { $ne : '' } }
  

• $in, $nin
  desc is in [] (or not in [])

  { desc: { $nin : ['', null] } }
  

• $regex : 정규 표현식
  해당 단어를 포함하는지 확인 가능

  { 'title' : { $regex : 'shaver' } }
  

Data export / import

• export

  mongoexport -h 127.0.0.1:27000 -d dbName -c collectionName -o filename.json
  

• import

  mongoimport -h 127.0.0.1:27017 -d dbName -c collectionName --file filename.json
  

Table of Contents

1. Headers
2. Block Quote
3. List
   • Ordered List
   • Unordered List
4. Code
5. 수평선
6. Links
7. 강조
8. Images

1. Headers

# This is a H1
## This is a H2
### This is a H3
#### This is a H4
##### This is a H5
###### This is a H6

This is a H1

This is a H2

This is a H3

This is a H4

This is a H5

This is a H6

2. Block Quote

> This is a blockquote.
>> This is a blockquote.
>>> This is a blockquote.

This is a blockquote.

This is a blockquote.

This is a blockquote.

3. List

3-1 Ordered list

1. 첫번째
2. 두번째
3. 세번째

1. 첫번째
2. 두번째
3. 세번째

3-2 Unordered list

* 빨강
  * 녹색
    * 파랑

+ 빨강
  + 녹색
    + 파랑

- 빨강
- 녹색
- 파랑

• 빨강
  • 녹색
    • 파랑
• 빨강
  • 녹색
    • 파랑
• 빨강
• 녹색
• 파랑

4. code

` 3개 연속으로 입력 후 코드 입력하면 됨. (코드 끝나면 ` 3개)

```
print(‘hello world’)
```

print('hello world')

5. 수평선

아래 줄은 모두 수평선을 만든다. 마크다운 문서를 미리보기로 출력할 때 페이지 나누기 용도로 많이 사용한다.

* * *
또는,
***
또는,
*****

6. Links

[link keyword][id]
[id]: URL

url

새 탭에서 여는 방법:

[link keyword][id]{:target='_blank'}
[id]: URL

new tab

인라인 링크 : [title](link url)

inline link

7. 강조

*single asterisks*
_single underscores_
**double asterisks**
__double underscores__
++underline++
~~cancelline~~

single asterisks
single underscores
double asterisks
double underscores
++underline++
cancelline

8. Images

![Alt text](/public/img/machine.jpg)
![Alt text](/public/img/machine.jpg "Optional title")

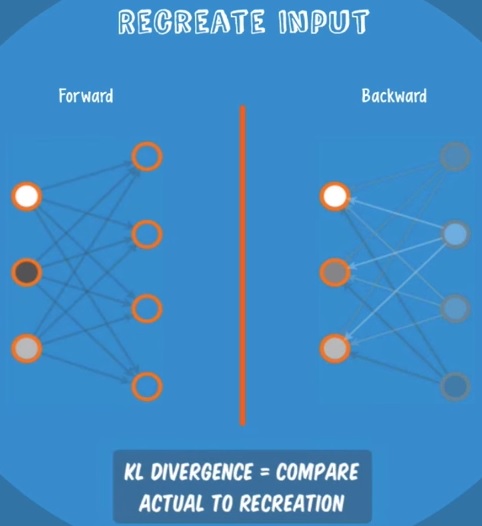
제한된 볼츠만 머신

데이터를 재구성(reconstruct) 함을 통해 입력 데이터의 패턴을 찾아내는 모델.

• Geoff Hinton 교수가 제안
• Vanishing Gradient 에 대한 해결 방안으로 사용 가능
• Unsupervised
• Feature extractor 의 일종이라고 할 수 있다.
  • 데이터에 내재한 패턴을 찾아냄.
• auto encoder 와 유사함.
• Shallow 2-layer net 이다.
  • visible layer
  • hidden layer

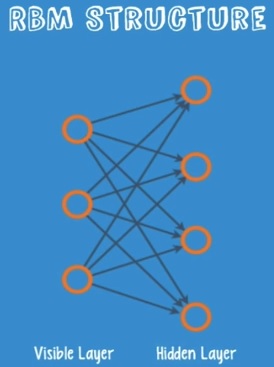
Recontruction

forward / backward 를 반복적으로 학습시켜 data 의 숨겨진 feature 들을 학습시킨다.
loss 는 KL Divergence 를 사용.