CRF(Conditional Random Field)

CRF 란?

저스틴 비버의 하루 일상을 순서대로 찍은 사진들이 있다고 상상해보자.
우리는 각각의 사진에 한 단어로 설명(라벨)을 달고자 한다. (예> 식사 사진, 수면 사진, 운전 중 등등)
어떻게 하면 될까?

한가지 방법은 사진들이 가지는 순서에 대한 정보는 무시하고 각 사진 자체만으로 분류를 해보는 것이 될 수 있겠다. 예를 들어 라벨이 달린 한 달 치의 사진이 주어졌다고 하면, 아침 6시 쯤에 찍힌 어두운 사진들은 ‘수면’ 과 연관이 있는 사진들이고, 밝은 색깔이 많이 포함된 사진은 ‘춤’ 에 대한 사진, 자동차가 나온 사진들은 ‘운전’ 사진이라는 등의 사실을 배울 수 있을 것이다.

하지만 순서에 대한 관점을 무시하면 많은 양의 정보를 잃게 된다. 예를 들어 입만 크게 나온 사진이 있다고 하자. 그건 노래하는 사진일까 밥 먹는 사진일까? 만약 이전의 사진이 저스틴 비버가 밥을 먹거나 요리하는 사진이었다면, 그 입 사진은 ‘먹는’ 행위에 관한 사진일 가능성이 더 높을 것이다. 하지만 이전 사진이 저스틴 비버가 노래나 춤 추는 사진이었다면, 입 사진도 마찬가지로 ‘노래하는’ 사진일 가능성이 높다.

Part-of-Speech Tagging

part-of-speech tagging 를 예로 좀 더 자세히 살펴보도록 하자.
POS tagging 의 목적은 한 문장의 어휘들의 품사를 달아주는 것이다. (ex> 명사, 동사, 형용사, 명사)
예를 들어 ‘Bob drank coffee at Starbucks.’ 라는 문장은 ‘Bob(명사) drank(동사) coffee(명사) at(전치사) Starbucks(명사)’ 가 될 것이다. 그럼 이제 CRF 를 이용해서 POS tagging 을 해보자. 먼저 다른 classifier 들과 마찬가지로 feature function $f_i$ 들을 정의해야 한다.

Feature functions in a CRF

CRF 에서 각각의 feature function 은 아래와 같은 입력들을 받는 함수이다:

• s : 문장
• i : 단어의 문장 내 인덱스
• $l_i$ : 현재 단어의 라벨
• $l_{i-1}$ : 이전 단어의 라벨

그리고 출력 값은 실수 값이 된다.(하지만 실제로는 0 또는 1 인 경우가 많다.)

참고 : 본 포스팅에서는 문장 전체에 대한 라벨이 아니라 현재 단어와 이전 단어의 라벨만 사용하도록 제한하고 있다. 이것은 linear-chain CRF 의 일종이라고 할 수 있다. 설명의 편의를 위해 범용적인 CRF 에 대한 내용은 생략하고자 한다.

Feature 를 Probabilties 로.

이제 각각의 feature function $f_j$ 에 weight $\lambda_j$ 를 할당해 보자.(데이터로부터 이 weight 들을 어떻게 학습하는 지는 아래에 설명하겠다.)
문장 s 가 주어졌을 때, 문장 내 모든 단어에 대한 weighted feature 값을 더하여 s 에 라벨 l 이 부여될 수 있는지 점수를 매길 수 있다.

(첫 번째 시그마는 각각의 feature function $f$ 에 대한 것이고, 안쪽 시그마는 $i$ 위치의 단어 각각에 대한 연산이다.)

그 다음 지수 연산(exponentiating)과 정규화(normalizing)를 통해 이 점수를 확률 $p(l | s)$ 로 환산할 수 있다.

Feature Function 예시

그럼 이 feature function 들은 어떻게 생겼을까? POS tagging 의 feature 들은 다음과 같을 수 있다:

• $$f_1(s, i, l_i, l_{i-1}) = \begin{cases} 1 & \mbox{if }l_i = \text{부사(ADVERB)} \mbox{ and the ith word ends in “-ly”} \\ 0 & \mbox{otherwise.} \end{cases}$$
  • 이 feature 에 대한 weight $\lambda_1$ 값이 양수이고 큰 경우, 이 feature 는 -ly 로 끝나는 단어를 ‘부사’ 로 라벨링할 거라는 의미가 될 것이다.
• $$f_2(s, i, l_i, l_{i-1}) = \begin{cases} 1 & \mbox{if } i = 1, l_i = 동사(VERB), \mbox{ and the sentence ends in a question mark} \\ 0 & \mbox{otherwise.} \end{cases}$$
  • 마찬가지로 feature 에 대한 weight $\lambda_2$ 값이 양수이고 큰 경우, ? 로 끝나는 문장의 첫 단어를 ‘동사’ 로 라벨링하고자 할 것이다.
• $$f_3(s, i, l_i, l_{i-1}) = \begin{cases} 1 & \mbox{if }l_{i-1} = \mbox{형용사(ADJECTIVE)} \mbox{, and }l_i = \mbox{명사(NOUN)} \\ 0 & \mbox{otherwise.} \end{cases}$$
  • weight 가 양수 인 경우, 이 feature 는 형용사 뒤에는 명사가 온다는 것을 의미한다.
• $$f_4(s, i, l_i, l_{i-1}) = 1 \mbox{ if }l_{i-1} =\mbox{ 전치사(PREPOSITION) and }l_i = \mbox{전치사(PREPOSITION).}$$
  • 이 함수에 대한 음수의 weight $\lambda_4$ 는 전치사 뒤에는 전치시가 오면 안되다는 것을 의미한다. 따라서 그런 라벨링이 발생하지 않도록 할 수 있을 것이다.

이게 끝이다!
정리해보면 CRF 를 만들기 위해서는,

1. feature function 몇 개를 정의해주고, (feature function 은 전체 문장, 현재 위치, 그리고 주변의 라벨 값을 참조한다.)
2. weight 를 할당하고
3. 전체를 몽땅 더한 다음,
4. 필요하면 그 값을 확률로 환산하면 된다.

이제 CRF 이 다른 머신 러닝 기술들와 어떻게 다른지 비교해보도록 하자.

Smells like Logistic Regression…

CRF 의 아래 식은 왠지 친숙해 보일 수도 있다. 궁금하면 여기

왜냐하면 CRF 는 근본적으로 Logistic Regression 의 순차 버전(sequential version)이기 때문이다.

Logistic Regression 이 분류(claasification) 을 위한 log-linear 모델인데 반해,
CRF 는 순차적인 라벨링(sequential labels) 을 위한 log-linear 모델이다.

Looks like HMMs…

HMM(Hidden Markov Model) 도 POS tagging(또한 일반적인 순차 라벨링) 에 사용될 수 있는 모델임을 기억하자.
CRF 가 라벨링 점수를 계산하기 위해 여러 개의 feature function 을 다 같이 사용하는데 비해,
HMM 은 라벨링을 위해 생성적(generative) 방식을 취한다. 그 식은 아래와 같다:

이 때,

• $ p(l_i | l_{i-1})$ 는 전이 확률(transition probabilities) - 예> 전치사 뒤에 명사가 나올 확률
• $ p(w_i | l_i)$ 는 출력 확률(emission probabilities) - 예> ‘명사’ 라벨이 ‘아빠’ 를 도출할 확률

그럼 HMM 과 CRF 는 어떻게 다른가?
CRF 가 더 강력하다!
CRF 는 HMM 이 할 수 있는 모든 것을 모델링할 수 있고, 그것보다 더 많은 일을 해낸다. 왜 그런지는 아래를 살펴보자.

HMM 확률 식에 log 를 취하면 아래와 같다.

이 log-확률을 2진(binary) 전이, 출력 feature 들에 할당된 weight 라고 간주하면, 위 식은 CRF 의 log-linear 형태와 완전히 일치한다. 다시 말해, 어떠한 HMM 이라도 그와 동일한 CRF 를 구현할 수 있다는 뜻이다. 그 방법은 아래와 같다.

• HMM 의 전이 확률 $p(l_i = y | l_{i-1} = x)$ 각각에 대해 CRF 전이 feature 를 아래처럼 정의한다.
  $f_{x,y}(s, i, l_i, l_{i-1}) = 1 \text{ if }l_i = y \text{, and }l_{i-1} = x$
  그리고 각 feature 에 다음과 같은 weight 를 부여한다.
  $w_{x,y} = \log p(l_i = y | l_{i-1} = x)$
• 위와 유사하게, HMM 의 출력 확률 $p(w_i = z | l_{i} = x)$ 각각에 대해 CRF 출력 feature 를 아래처럼 정의한다.
  $g_{x,y}(s, i, l_i, l_{i-1}) = 1 \text{ if }w_i = z\text{, and }l_i = x$
  그리고 각 feature 에 다음과 같은 weight 를 부여한다.
  $w_{x,z} = \log p(w_i = z | l_i = x)$

그러면 이 feature function 들을 사용하여 계산된 $p(l|s)$ 점수는 해당하는 HMM 에 의해 계산된 점수에 정확히 비례하게 되고, 따라서 모든 HMM 은 특정 CRF 로 표현이 가능해진다.

하지만 CRF 훨씬 풍부한 라벨 분포 set 를 모델링할 수 있는데, 이 이유는 다음과 같다.

• CRF 는 훨씬 많은 수의 feature set 를 정의할 수 있다. HMM 은 태생적으로 지엽적(local) 속성을 가진다. 왜냐면 HMM 은 2진 전이, 출력 feature function 만 사용 가능하고, 이로 인해 각 단어는 오직 현재의 라벨에, 그리고 각 라벨은 바로 이전의 라벨에만 의존하게 되기 때문이다. 이에 반해 CRF 는 좀더 전역적(global) feature 들을 사용할 수 있다. 예를 들어 위에서 보여준 POS tagger 의 feature 들 중 하나는 문장의 끝이 ? 인 경우 문장의 제일 첫 단어가 동사 로 태깅될 확률을 높이고 있다.
• CRF 는 임의(arbitrary)의 weight 값들을 가질 수 있다. HMM 의 확률 값들은 어떤 조건 - 예를 들면, $ 0 <= p(w_i | l_i) <= 1, \sum_w p(w_i = w | l_1) = 1$ - 을 반드시 충족시켜야만 한다. 그에 비해 CRF 의 weight 는 아무 제약이 없다.
  $\log p(w_i | l_i)$ 는 어떠한 값이든 될 수 있다.

Weight 의 학습

CRF 에서 weight 를 어떻게 학습시키는지에 대한 질문으로 다시 되돌아가자. gradient ascent (짜잔) 를 사용하는 것이 하나의 방법이 될 수 있다.

학습 데이터(문장들과 그에 대한 POS 라벨들)가 충분히 있다고 가정해보자. 먼저 CRF 모델의 weight 들을 임의의 값으로 초기화 한다. 이 무작위 weight 값들을 정답으로 바꿔나가려면 각각의 학습 데이터에 다음과 같은 작업을 해주면 된다.

• 각각의 feature function $f_i$ 에서 학습 데이터의 log 확률에 대한 gradient 를 계산한다. $\lambda_i \text{ : }\frac{\partial}{\partial w_j} \log p(l | s) = \sum_{j = 1}^m f_i(s, j, l_j, l_{j-1}) - \sum_{l’} p(l’ | s) \sum_{j = 1}^m f_i(s, j, l’_j, l’_{j-1})$
• gradient 의 첫 번째 term 은 true 라벨을 갖는 feature $f_i$ 의 분포를, 두 번째 term 은 현재 모델에서 feature $f_i$ 의 expected 값의 분포를 나타냄을 주목하자.
• $\lambda_i$ 를 gradient 방향으로 이동시킨다 :
  $\lambda_i = \lambda_i + \alpha [\sum_{j = 1}^m f_i(s, j, l_j, l_{j-1}) - \sum_{l’} p(l’ | s) \sum_{j = 1}^m f_i(s, j, l’_j, l’_{j-1})]$ where $\alpha$ is some learning rate.
• 특정 조건(더 이상 갱신이 안된다던가)에 도달할 때까지 위의 작업을 반복한다.

최적 라벨 찾기

우리의 CRF 모델을 학습시켰고 이제 새로운 문장이 입력된다고 생각해보자. 라벨링은 어떻게 되나?

단순한 방법은 모든 가능한 라벨 l 에 대한 $p(l | s)$ 를 계산하고, 이 확률을 최대화 시키는 라벨을 고르는 것이 될테다. 하지만 m 길이의 문장과 k 개의 tag 셋이 있다면 총 $k^m$ 개의 조합이 가능하기 때문에, 이 방식은 지수승의 연산을 필요로 한다.

더 좋은 방법이 있다. (linear-chain) CRF 는 optimal substructure 속성을 만족하기 때문에, (polynomial-time 복잡도의) 동적 프로그래밍 알고리즘으로 최적 라벨을 찾을 수 있다. 이는 HMM 에 Viterbi 알고리즘을 적용하는 것과 유사하다.

좀 더 재밌는 응용

사실 part-of-speech tagging 은 좀 지루하고, 다른 POS 태거도 이미 많다. 실 생활에서 CRF 는 어디다가 써먹을 수 있을까?

트위터에서 사람들이 크리스마스에 받은 선물의 타입을 마이닝하고 싶다. 고 해보자.

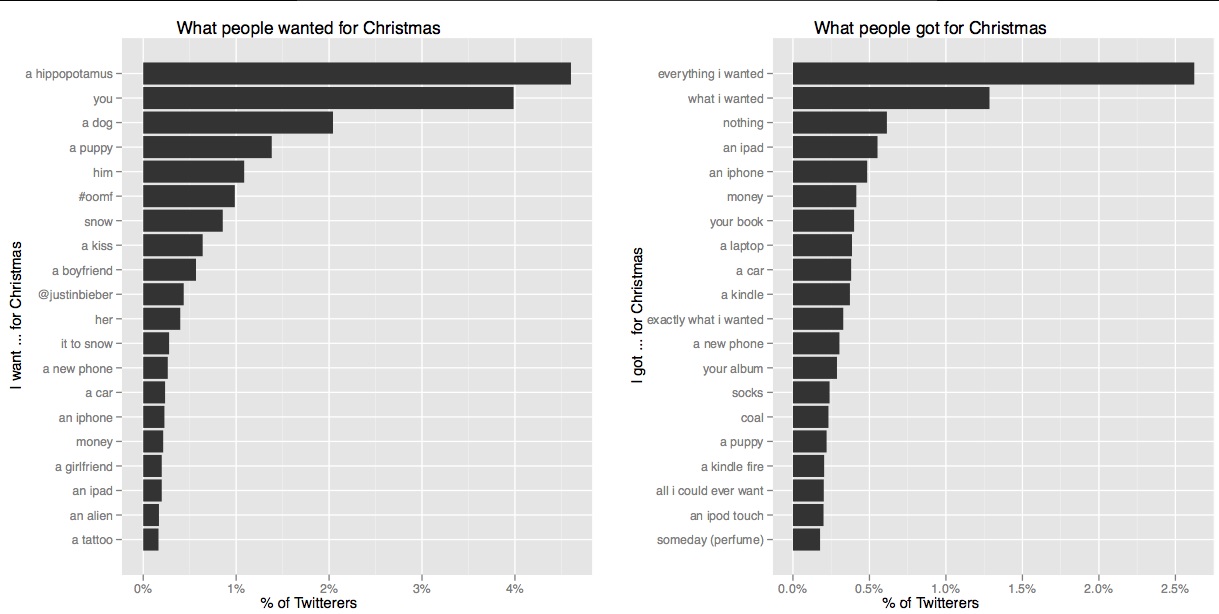
그러면 문장에서 어느 단어가 선물에 해당하는지 어떻게 찾아낼 수 있나??!!1

위와 같은 그래프를 만들기 위해 나는 그냥 “크리스마스에 XXX 가 갖고싶어요.” 와 “크리스마스에 XXX 를 받았어요!” 형태의 문장을 검색했을 뿐이다. 하지만 더 세련된 CRF 버전으로, part-of-speech 에서의 품사 같이 GIFT 라는 태그 (한 발 더 나가면 GIFT-GIVER, GIFT-RECEIVER 를 이용해 선물을 준사람과 받은사람의 정보까지) 를 사용해서 이것을 POS 태깅 문제처럼 해결해 볼 수 있을 것이다. 그 때 feature 는,

• “이전 단어가 GIFT-RECEIVER 이고 그 이전 단어가 ‘gave’ 라면, 현재 단어는 GIFT 임”
• “다음 두 단어가 ‘for Christmas’ 면 현재 단어는 GIFT 임”

와 같은 형태가 될 수 있을 것이다.

마무리

좀더 ‘랜덤한’ 생각을 나열하고 끝내고자 한다.

• 이 포스트에서는 CRF 를 사용한 그래픽 모델 프레임웍에 대한 내용은 일부러 스킵했다. 왜냐면 CRF 의 기본을 이해하는데는 큰 도움이 되지 않기 때문이다. 하지만 더 알고싶다면 Daphne Koller 가 공짜로 가르쳐주는 온라인 강좌를 들어보시길.
• 아니면 CRF 를 적용한 많은 NLP 응용 분야(POS 태깅이나 named entity extraction등)에 관심이 있다면 Manning 과 Jurafsky 가 강의를 하고 있다. (링크가 있었는데 깨짐. http://www.nlp-class.org)
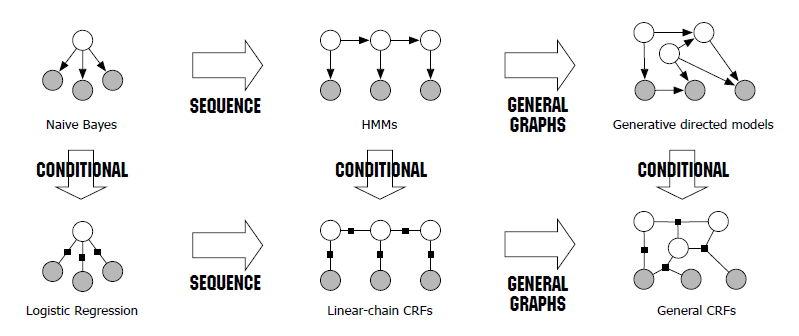
• 또한 CRF/HMM 과 Logistic Regression/Naive Bayes 간의 유사점에 대해 조금 더 꾸며봤다. 아래 이미지를 참고바람.

출처 : introduction to conditional random fields