Monte Carlo Method

정의

난수를 이용하여 함수의 값을 확률적으로 계산하는 알고리즘.

핵심 아이디어

이론상 determistic 할지도 모르는 문제에 대해 randomness 를 사용하여 해결한다!

주로 물리/수학적 문제들에 대해 다른 방법으로 해결할 수 없는 경우에 사용한다.(ㅋㅋ)

주요 적용 분야

1. 최적화 문제
2. numerical integration (수치적 미분?)
3. 확률 분포로부터 draw 를 생성 (generating draw from probability distribution)

어떻게 동작하나?

일반적으로 아래 패턴으로 동작함.

1. 입력 가능한 데이터의 도메인을 정의한다.
2. 해당 도메인에 대한 확률 분포로부터 랜덤 데이터를 생성
3. 입력 데이터에 대한 deterministic 계산을 수행
4. 결과 수집

예를 들어, (x,y) 그래프의 1 사분면에 (0, 0) 을 중점으로 하고 반지름이 1 인 원이 있다고 생각해보자. 원의 넓이는 π/4 일 것이다.
이 때 Monte Carlo Method 를 이용해 π 값을 근사해 보면,

1. 한 변의 길이가 1인 정사각형을 그리고, 그 안에 반지름이 1 인 원을 그린다. (1/4 원)
2. 균등한 크기의 물체를 사각형 안에 균등하게 흩뿌린다.(uniformly scatter)
3. 원 안에 들어간 물체의 갯수와 전체 갯수를 센다.
4. 원 안에 들어간 물체의 갯수와 전체 갯수의 비율은 두 영역의 비율과 같으므로, 즉 π/4 가 된다.
   해당 비율에 4을 곱해서 π 의 근사치를 구할 수 있다.

여기서 중요한 포인트 2가지.

1. 흩뿌릴 때 균등하게 분포되지 않으면 결과가 좋지 않을 것이다.
2. 입력 데이터의 갯수가 많아야 한다. 많을 수록 결과가 개선될 것이다.

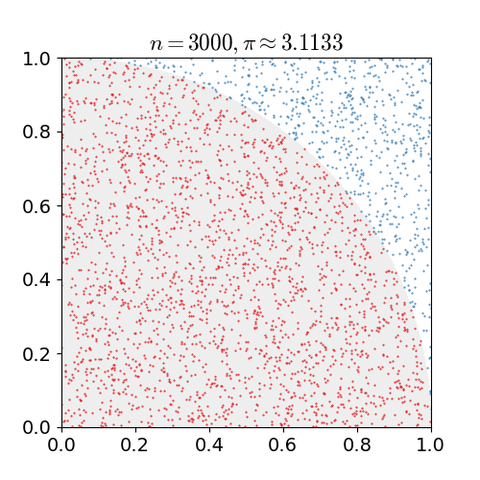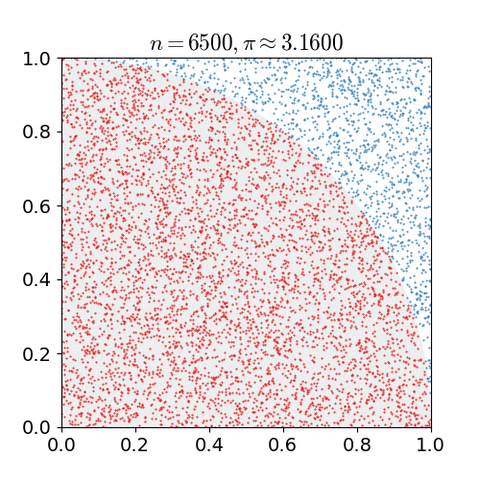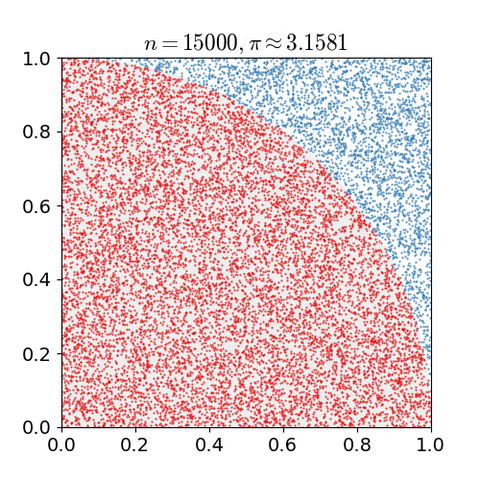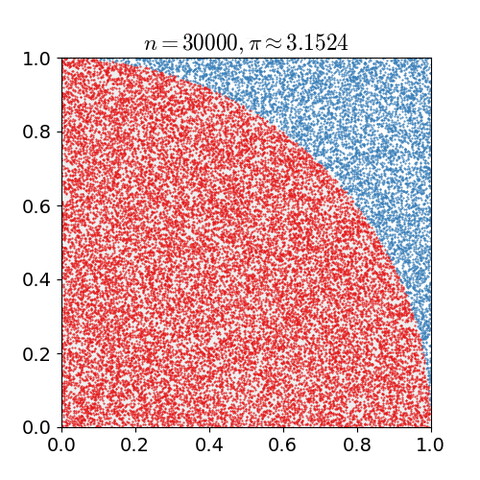
Monte Carlo Method 를 적용하기 위해서는 많은 수의 랜덤 값들이 요구되는데, 이로 인하여 pseudorandom number generator 의 개발에 박차를 가하게 되었다. pseudorandom number generator 는 기존에 통계적 샘플링에서 주로 사용되던 랜덤 숫자 테이블(table of random numbers) 대비 훨씬훨씬 성능이 좋았다.

출처 : Monte Carlo method